ทฤษฏีคอมพิวเตชั่น CT313
Original form MODULE P220
Theory of Computation 2001 http://web.cs.city.ac.uk
Topic 6: Turing Machines

Contents

  1. Turing Machines
  2. Subprograms in Turing Machines
  3. Non-Termination
  4. Recursively Enumerable Languages
  5. Applications of Turing Machines

Turing Machines

We have now studied of two classes of machine Ñ FSA and PDA, and their corresponding classes of language Ñ regular and context-free.
We have also discovered that some languages, the non-context-free, are not recognisable even by non-determinstic PDAs.
The next class of machine is more powerful still.
In fact, it is the most powerful of all computational machines -- if a Turing Machine cannot compute it, it is not computable!
This model of computation was developed by Alan Mathison Turing, who also developed the first electronic computer, Colossus, for breaking the German militery codes during the Second World War.

Definition

A Turing Machine (TM) is a collection of six things:

  1. A finite input alphabet, comprising those symbols that may be read from
  2. a tape, which is divided into a sequence of numbered cells each containing one symbol or a blank. The input word is presented to the machine one symbol per cell, beginning in the leftmost cell. The rest of the tape is initially blank (represented by the character /\).
  3. A tape head that can, in one step, read the contents of a cell on the tape, replace it with another (or the same) symbol and reposition itself to the next cell to the right or left of the one it has just read.
  4. A finite output alphabet comprising those symbols that can be written to the tape by the tape head. This can include symbols from the input alphabet.
  5. A finite set of states including exactly one start state and some halt states that cause execution to terminate.
  6. A program which is a set of rules that tell the machine, on the basis of its current state and the symbol in the cell currently under the tape head, what its next state should be, what it should write in the current cell and how to move the tape head.  If the tape head ever reads some symbol for which no rule is provided in the current state, then the machine crashes, that is, stops without reaching one of its halt states. A crash also occurs when the first cell of the tape is under the tape head and the current rule tells the machine to move LEFT.

Example

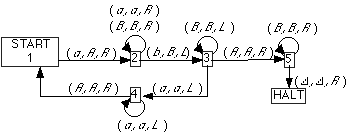
The following TM accepts the language L = anbn.

You may find it easier to understannd this graphical notation if you compare it to the following representation in tabular form of the same TM:

From State To State Read Write Move Head
1 2 a A Right
2 2 a a Right
2 2 B B Right
2 3 b B Left
3 3 B B Left
3 5 A A Right
3 4 a a Left
4 4 a a Left
4 1 A A Right
5 5 B B Right
5 HALT /\ /\ Right

We can trace the behaviour of this machine on the tape aabb, as follows:
 

State Tape Contents
1 aabb
2 Aabb
2 Aabb
3 AaBb
4 AaBb
1 AaBb
2 AABb
2 AABb
3 AABB
3 AABB
5 AABB
5 AABB
5 AABB/\
HALT AABB/\ /\

Self Assessment Exercise

Trace the behaviour of this machine on the tape aaabb.
Back to Topic 6

Subprograms in Turing Machines

When designing a Turing Machine torecognise some language, it is usually necessary to write markers to the tape so that the machine can scan up or down the tape for some pattern of symbols and then return to the position it started from.
That was the purpose of the As and Bs in the TM for anbn above.
Such markers can often be thought of as 'brick walls' that fence off some section of the tape being processed so that the TM 'bounces' off them as it moves up and down the tape.
Often, we need to INSERT a marker symbol on the tape at exactly the point where the tape head is currently located without overwriting the symbol already there. This involves shifting all the symbols after the current tape head position one position to the right to make room for the marker, leaving contents of the tape before that position unchanged.
The part of the TM program that achieves this effect is independent of the rest of the program.
It is an independent subprogram which, once written, can be incorporated into any other TM program (with an appropriate tape alphabet) by indicating where we want it to be invoked and what symbol we want it to insert.
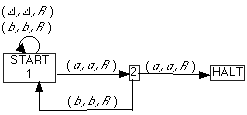
Symbolically, the call to INSERT, say, the symbol a would appear in the calling TM as

If this call to INSERT was made when the tape and its head was in the condition, say:

aabbaa

then the condition after its call would be

aababaa

The TM for the subprogram INSERT a, with the alphabet {a, b},  looks like this:

Self Assessment Questions

  1. Construct a TM subprogram, with alphabet {a, b}, that performs the operation DELETE, which deletes the symbol currently under the tape head by shifting all the symbols after it one position to the left, leaving the tape head positioned at the symbol immediately following the one deleted. For example, invoking DELETE on a tape in the condition ababa would leave it in the condition abba.
  2. Construct a TM that recognises the language EQUAL, whose words are all strings of the alphabet {a, b} that have equal numbers of as andbs, by INSERTing a * symbol before the beginning of the input string and then repeatedly scanning up the tape, DELETEing one a and one b on each pass and returning to the * symbol to start the next one. With this algorithm, the TM should ACCEPT a string when it detects a blank cell immediately after the * at the beginning of a pass.
  3. Test the performance of both your answers by tracing your TMs on suitable test strings.

Back to Topic 6

Non-Termination

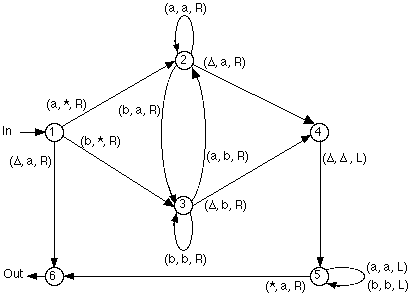
The following TM is supposed to accept all words with a double a in them somewhere.

This TM exhibits the following, rather problematic, behaviour:

Unlike an FSA or a PDA, a TM cannot just run out of input in some intermediate state.
There are always infinitely many blanks on a tape after the meaningful input has been exhausted.

Definition

Every TM T over the alphabet S  divides the set of strings S*  into three classes:

ACCEPT(T): the set of all strings leading to a HALT state. This is the language recognised by T.
REJECT(T): the set of all strings that cause T to crash during execution by being in a state that has no exit arc for the symbol currently under the tape head.
LOOP(T): the set of all other strings, that is, strings that loop forever while running on T.

Back to Topic 6

Recursively Enumerable Languages

Remember the Chomsky classification:

Languages that are accepted by FSAs are called regular languages.
Languages that are accepted by PDAs are called context-free languages.

What can we say about the class of languages accepted by TMs?

Definition

A language L over the alphabet S  is called recursively enumerable (r.e.) if there is a TM T that accepts every word in L and either rejects or loops for every word in L'.

We have seen that, for every TM,T, which runs on strings from the alphabet S,

 S*  = ACCEPT(T) + LOOP(T) + REJECT(T)

If we denote by L' the complement of a language, L, over its alphabet S (that is, the set difference S* - L), we can rewrite the condition in the defintion of r.e. as

ACCEPT(T) = L and
REJECT(T) + LOOP(T)  = L'

Definition

A language L over the alphabet S  is called recursive if there is a TM T that accepts every word in L and rejects every word in L', that is:

ACCEPT(T) = L  and
REJECT(T) = L'  and
LOOP(T)  = Ø

Note: Turing used the word recursive because he believed that any set defined by a recursive definition could be defined by a TM.

There is a subtle difference between languages that are recursive and those that are recursively enumerable (r.e.).
A TM might never reach a HALT state on an r.e. language, whereas it is guaranteed to do so for a recursive one.
Back to Topic 6

Applications of Turing Machines

In our earlier discussions of FSAs and PDAs, and of their respective language classes, we addressed two separate, but related, issues:

  1. How is the representation of a machine related to the representation of the language that it accepts?
  2. How can we prove that some language cannot be recognised by any machine of a given class?

The answers to both these theoretical questions are important  in practice.

The first provides the foundations for the important technology of language processing.

Although corresponding transformation systems exist for TMs and the recursive languages, no language processing technology uses them, becuase TM algorithms are not very effective when implemented as computer programs.
No software technology is founded on the theory of Turing Machines!
So why do we study them?
The answer lies in the second of the issues addressed above.
The Turing Machine is a model of computation in which the issue of computability itself can be studied.
If we can prove that some language cannot be recognised by a TM, then that language represents a function that cannot be computed at all.
We can therefore use the TM to study the limits of computability, which we will address in Topic 10.

Meanwhile, we will turn our attention to the question of computational complexity, which asks how hard it is to compute certain functions.
Back to Topic 6
Next Topic

Start of Module

If you have comments or suggestions, email to author at b.cohen@city.ac.uk
or me Vid-Com-Ram / members.tripod.com/bummerang


หมายเหตุ : เอกสารเวปหน้านี้นำมาจากมหาวิทยาลัยแห่งหนึ่งในประเทศอังกฤษ เป็นหลักสูตรคล้ายคลึงกับ CT313 นำมาเพื่อเป็นเอกสารเปรียบเทียบและอ้างอิง มิได้หวังผลประโยชน์ใดๆ และขอบอกว่าเค้ามีลิขสิทธิ์นะ