
The class of all languages recognisable
by Finite State Automata is known as the regular (or type3) languages.
Regular languages may be described by regular expressions (RE).

The RE for the language BI of Binary Integers is
which we may read as:
Every word in the language BI is either
Write down a RE for the language of Binary Fractions
Note that 'intermediate variables' may be freely introduced into the equations of REs, as in the following
The RE for the language DI of Decimal Integers is
which may be read as:
Every word in the language DI is either
We formalise this notion in the following

The above definition leaves open some important
These questions were answered by the logician
Stephen C. Kleene.
![]() Back
to Topic 2
Back
to Topic 2
Any language that can be defined by
can be defined by all three methods.
The proof is in three parts:
This is easy.
Every finite state automaton is representable by a corresponding transition graph.
Therefore any language that has been defined by a FSA has already been defined by a TG.
The proof of this part is by recursive definition and constructive algorithm:
Rule 1:
There is an FSA that accepts any particular letter of the alphabet.
There is an FSA that accepts only the empty string.Self Assessment Questions
Construct FSAs for each of the two cases in rule 1.
Rule 2:
If there is an FSA that accepts the language defined by the RE r
and there is an FSA that accepts the language defined by the RE s,
then there is an FSA that accepts the language defined by the RE (r+s).Self Assessment Questions
Construct FSAs for two simple REs and derive the FSA for their 'sum'.
Rule 3:
If there is an FSA that accepts the language defined by the RE r
and there is an FSA that accepts the language defined by the RE s,
then there is an FSA that accepts the language defined by the RE rs.Self Assessment Questions
Construct FSAs for two simple REs and derive the FSA for their 'concatenation'.
Rule 4:
If there is an FSA that accepts the language defined by the RE r,
then there is an FSA that accepts the RE r*.Self Assessment Questions
Construct FSAs for two simple REs and derive the FSA for their 'closure'.
End Proof
The proof of this part provides a constructive algorithm that will transform every conceivable TG into an equivalent RE in a finite number of steps.
Step 1: Single Start State
A TG may have many start states.
We simplify such a TG by defining a single start state from which a transition, labeled with the symbol for the null string, is constructed to each state that was a start state of the original graph (but is not a start state of the new one), thus:

Step 2: Single Accepting State
Similarly, a TG with more than one accepting state can be transformed to an equivalent graph with a single accepting state to which an arc, labeled with the symbol for the null string, is constructed from each accepting state of the original graph, thus:

Step 2a: No Transitions into Start State or out of Final State
This rule eliminates loops at the start and end by introducing, if necessary, a new start state with a null transition to the original one , and/or a new accepting state with a null transition from the original one.
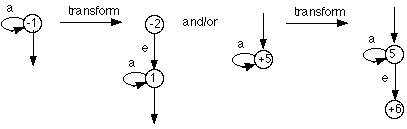
Step 3: Regular Expressions on Edges
Next we build up, piece by piece, a RE that defines the same language as the TG.
Previously, we allowed the edges of the graph to be labeled only with strings of symbols from the alphabet.
However, since every string can itself be thought of as a RE, we now allow REs themselves to label edges of the graph.Step 3.1: Sum Loops
Consider a state with an edge looping back to itself.
However many different edges like this that there are on a given state, they can always be reduced to just one edge, the REs on those edges being summed, thus:

Step 3.2: Sum Edges
Similarly, two states that are connected by more than one edge going in the same direction can be reduced to just one edge, labelled by a summation, thus:

Step 3.3: Bypass States
The bypass operation is used progressively to reduce the TG to a RE: thus:

Here, the removal of state 2 from the graph breaks a path that leads from state 1 to state 3.
This path must be restored, and labelled with the appropriate RE, in this case ab, if the new graph is to be equivalent to the original.
When performing a bypass transformation, remember to account for all such broken paths, and no others.
If the bypassed state has an arc to itself (i.e. a loop) then the RE on that loop is Kleene starred, thus:
Given any TG, one may derive a Regular
Expression for the language recognised by the FSA that the TG represents by
applying appropriate steps of Kleene's theorem, successively reducing
the graph until it consists of exactly one start state and one accept state.
At that point, the arc between those states will have become labelled by the
required regular expression.
Derive a Regular Expression for the language
recognised by the following Transition Graph by applying an appropriate sequences
of transformations, each of which is a step in Kleene's Theorem.
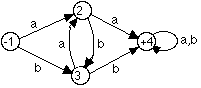
We will describe the steps in sequence here.
You should draw the succesive graphs yourself as as a Self Assessment Exercise.
Step 1 is not applicable here because there
is already only one start state (1).
Step 2 is not applicable here because there is already only one accept state
(4).
Step 2a is applicable because the start state (1) has two arcs leaving it and
the accept state (4) has two arcs entering it.
We therefore introduce null transitions from a new start state (say, 5) to a
new final state (say, 6) amd remove the start\final state indications from states
1 and 2.
Now we can apply Step 3.1 to sum the loops on state 4, which transforms the decoration on the loop from "a,b" to the RE "a+b".
Step 3.2 is not applicable here because there is no pair of arcs between the same states in the same direction.
Step 3.3 is applicable here, and
the only choices (that do not reintroduce multiple arcs on the start and accept
states) are to bypass state 2 or to bypass state 3.
Let's choose (arbitrarily) to bypass state 2.
This breaks four paths:
from state 1 to state 3, which requires the RE "ab",
from state 1 to state 4, which requires the RE "aa",
from state 3 to state 4, which requires the RE "aa", and
from state 3 to itself, which requires the RE "ab".
We remove the broken paths, and state 2,
from the TG and insert the new paths with their REs.
Note the difference between the sum "a+b" on the loop at state 4 and
the concatenation "ab" on the loop at state 3.
Now we can apply Step 3.2 to sum the arcs from state 1 to state 3, giving "ab+b", and the arcs from state 3 to state 4, giving ""aa+b", because they run in the same direction.
Now we can apply Step 3.4 to bypass state
3, including the loop on it.
This breaks one path from state 1 to state 4, which requires the RE "(ab+b)(ab)*(aa+b)".
Note how:
the whole RE labelling the loop on state 3 is enclosed within the Kleene star, and
parentheses are needed to disambiguate the new RE on the lower arc from state 1 to state 4.
Now we can apply Step 3.2 again to sum
the arcs from state 1 to state 4, because they run in the same direction, giving
a single arc from state 1 to state 4 labelled with the RE "aa+(ab+b)(ab)*(aa+b)".
Noe we can remove state 4, together with the loop on it. This breaks one path
from state 1 to state 6 which requires the RE "(aa+(ab+b)(ab)*(aa+b))(a+b)*".
Note that the null transition, that we introduced from state 4 to state 5, vanishes
again, because concatenating the null string to any RE does not alter it.
And finally, we can apply Step 3.2 again
to bypass state 1. This breaks one path from state 5 to state 6 but does not
change the RE because the path from state 1 to state 5 was labelled with the
null string.
We now have a TG with a single start state (5), a single final state (6) and
a single arc between them.
The label on this arc is the RE "(aa+(ab+b)(ab)*(aa+b))(a+b)*", which
describes the same language as the original TG, as required.
So far, out machines have all been language
acceptors, but it is possible to have FSAs which also produce outputs.
A Moore Machine is a collection of five things:
The input and output alphabets are not necessarily the same.
The Mealy Machines are similar, but their outputs are generated during transitions. The output alphabet therefore labels arcs rather than states.
It can be shown that Moore and Mealy
machines are equivalent, that is, that the behaviour of every Moore machine
may be simulated by a Mealy machine, and vice versa.
![]() Back
to Topic 2
Back
to Topic 2
![]() Next
Topic
Next
Topic
If you have comments or
suggestions, email to author at b.cohen@city.ac.uk
or me Vid-Com-Ram
/ members.tripod.com/bummerang
หมายเหตุ : เอกสารเวปหน้านี้นำมาจากมหาวิทยาลัยแห่งหนึ่งในประเทศอังกฤษ
เป็นหลักสูตรคล้ายคลึงกับ CT313 นำมาเพื่อเป็นเอกสารเปรียบเทียบและอ้างอิง มิได้หวังผลประโยชน์ใดๆ
และขอบอกว่าเค้ามีลิขสิทธิ์นะ