ทฤษฏีคอมพิวเตชั่น CT313
Original form MODULE P220
Theory of Computation 2001 http://web.cs.city.ac.uk
Topic 5: Push Down Automata and the Pumping Lemma for CFGs

Contents

  1. Push-Down Automata
  2. Push-Down Automata and CFGs
  3. The Pumping Lemma for CFLs

Push-Down Automata

Imagine an intuitive design for a machine that will accept the language L = anbn.
Suppose that this machine has a stack with an infinite capacity.
When presented with a word at its input, it reads the symbols one at a time.
For each a that it reads, it pushes some symbol, say *, onto the stack until it reaches a b, then it  pops one * off the stack for each b that it reads.
If the stack is empty when no bs are left, then there must have been an equal number of as and bs.
This machine could therefore accept all words of L and reject all words not in L.
That is, it could recognise L, which we know to be context free.
The class to which this machine belongs is the Push Down Automata (PDA).
As before, we will start our investigation of this class of machine with a formal definition:

Definition:

A Pushdown Automaton  (PDA) is a collection of eight things:

  1. An alphabet of input symbols.
  2. An input tape (infinite in one direction). The string of input symbols is placed on the tape starting in some known cell and the rest of the tape is known to be blank.
  3. An alphabet of stack symbols.
  4. A pushdown stack (infinite). Initially, it contains a blank character.
  5. One start state.
  6. Halt states of two kinds: some accept and some reject.
  7. Push states that introduce characters onto the top of the stack.
  8. Finitely many branching states of two kinds:

Example

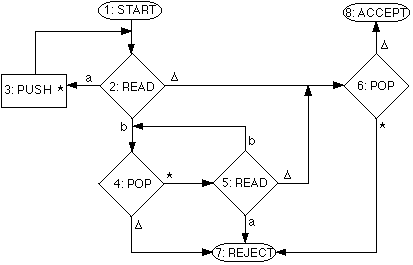
The PDA described above that recognises anbn has the input alphabet  {a,b}, the stack alphabet {*} and the following state transition diagram:

To trace the behaviour of a PDA when presented with an input string, we need to keep records of:

For example, the behaviour of the above PDA on the string aabb is traced in the following table, where the position of the read head in the input string is shown by underlining the current character, and values of the read head position and stack contents are shown on entry to the state:
 

State Read Head Stack
1 aabb/\ /\
2 aabb/\ /\
3 abb/\ /\
2 abb/\ */\
3 bb/\ */\
2 bb/\ **/\
4 b/\ **/\
5 b/\ */\
4 /\ */\
5 /\ /\
6 /\ /\
7 /\ /\

The string aabb is accepted, as it should be.
Notice that this PDA is deterministic. In each decision state (READ or POP), there is no more than one outgoing arc for each symbol.
We can represent non-deterministic PDAs (NPDA) using the same notation. As before, the non-determinism is interpreted as allowing the PDA to choose among the possible outgoing arcs. We will see NPDAs in action later.

Self Assessment Questions

Trace the behaviour of this PDA on the strings:

  1. aaabb
  2. aabbb

Back to Topic 5

Push-Down Automata and CFGs

We have already proved that the FSA class of machines is coincident with the RL class of languages.
That is, every Regular Language can be recognised by some FSA.
We have just seen that at least one CFL ( anbn) can be recognised by a PDA, but do these clases coincide, that is:

Can every context free language be recognised by some PDA?

As before, we will prove that this is in fact the case by a constructive algorithm that generates, for any CFL,
a NPDA that recognises it.

Step 1

Construct a CFG for the lanaguage.

Step 2

Convert that CFG to CNF.

Step 3

Construct the PDA as follows:

State 1: push the start symbol (conventionally 'S')
State 2: pop the stack, branching to:

one state for each occurrence of each non-terminal on the left hand side of the CFG, and
one state for the empty stack;

State n (one for each occurence each non-terminal):

if the corresponding right hand side is a (single) terminal symbol

then read the next character from the tape and
if it is equal to the terminal symbol from the CFG

then branch to State 2
else REJECT

else (the right hand side must be a pair of non-terminals)
push  the second non-terminal on to the stack,
push the first non-terminal on to the stack, and
branch to State 2

State k (for the empty stack):

read the next character from the tape and
if it is empty (denoted by l),

then ACCEPT
else REJECT

Example

The language Palindrome can be described by a CNF grammar as follows:

S -> AK | BL | AA | BB | a | b | /\
K -> SA
L  -> SB
A -> a
B -> b

By applying Step 3 of the above construction, we arrive at the following PDA that recognises Palindrome:

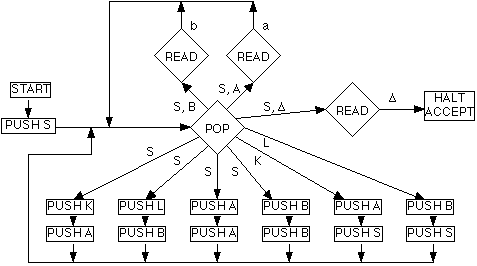
It is important to understand the non-deterministic character of this PDA.  It will reject a word, as not being a member of the language, only if none of the alternative paths through the machine reaches the HALT ACCEPT state.  You might imagine it as trying all its alternatives before giving up.
Note that, unlike the FSAs, there is no transformation between non-deterministic and deterministic PDAs.
NPDAs are more powerful than DPDAs.
The deterministic PDAs recognise a subclass of the context free languages, called LR(k), which are very important in the design of programming language compilers.

Self Assessment Questions

For each of the following CFGs, construct a PDA that recognises the language it generates, using the constructive algorithm.

We have now studied of two classes of machine Ñ FSA and PDA, and their corresponding classes of language Ñ regular and context-free.
We know that there is a class of languages, the context free languages, that can be recognised by PDAs but not by FSAs, and we have a technique - the Pumping Lemma - for proving that some language is not regular.
The obvious questions to ask now are

Back to Topic 5

The Pumping Lemma for CFLs

As before, the proof that a given language is not context-free is done by reductio ad absurdum, that is, we assume that the language is context-free and show, using a different  Ôpumping lemmaÕ, that this assumption leads to a contradiction.
In this case, we base our argument on the structure of an (imaginary) CFG for the language (in CNF), rather than the structure of an (imaginary) recognising machine.

Theorem

If G is any CFG in CNF with p productions
and w is any word generated by G with length greater than 2p,
then we can break w up into five substrings:

w = uvxyz  such that

x is not null  and
v and y are not both null

and such that all the words

uvnxynz   for n=1,2,3,...

can also be generated by G.

Proof

The proof relies on the observation that any CFG that generates an infinite language must contain a recursive non-terminal (just as an FSA for an infinite regular language must contain a loop).
Therefore, the corresponding context-free language must contain all the words generatable by unbounded recursion on that non-terminal.
We can see how this works by considering one specific derivation of the word w from the grammar G.
Suppose

that one of the recursive non-terminals in this grammar is P
that its first production rule is

P -> QR

and that the tree of productions that generates w looks like this


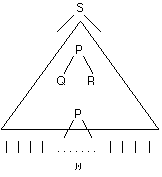
The triangle indicates the whole part of the tree generated from the first P down to where the second P is produced.
Now divide w into the following five substrings:

u is the substring generated to the left of the triangle (which may be null)
v is the (possibly null) substring descended from the first P but to the left of that generated by the second P
x is the (non-null) substring descended from the lower P
y is the (possibly null) substring descended from the first P but to the right of that generated by the second P
z is the substring generated to the right of the triangle (which may be null)

to get a picture like this

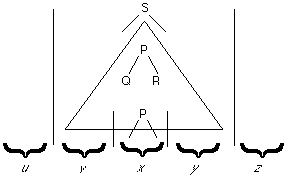
It is possible for either u or z or both to be null, and either v or y may be null, but not both.
Now consider what happens to the tree and to the generated word if we do one more iteration of the productions inside the triangle.
The new picture looks like this

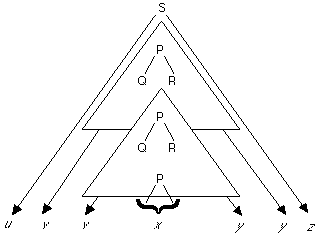
This generates the word uvvxyyz which is therefore in the language generated by G.
We can continue to pump the recursion in ths way. If we do it ntimes, we will generate the words

uvnxynz, for n = 1,2,3,...

all of which must be in the language generated by G.
QED

Example

Consider the CFG (in CNF):

S -> AB
B -> RC
R -> XT | z
T -> RY
A -> a
C -> c
T -> t
Y -> y

The generated language would contain the following words:

azc, axzyc, axxzyyc, axxxzyyyc, É  , axnzync, É and so on, for all n.

Notice where the strings are Ôpumped upÕ by the recursive non-terminal (R in this case).
The CFG pumping lemma states that all infinite context-free languages will contain infinite sequences of words in this kind of pattern.
Therefore, if an infinite language contains a word of this structure which, when appropriately ÔpumpedÕ, produces a word that is patently not in the language, that language cannot be context-free.

Worked Example

Show that the language L = anbncn,  for n=1,2,3,..., is  not context free.

Observe that all words in L have

exactly one two-symbol substring ab,  one bc, and
no two-symbol substrings ac, ba, ca, or cb.

Let w = uvxyz  be a word in L.
Now either

  1. v consists of a solid block of one symbol (a, b or c ) or
  2. v contains more than one symbol

(and similarly for y).
There are no other cases.
In the first case, some word uvnxynz will not have equal numbers of the three symbols a, b, c.
In the second case, some word in uvnxynz will contain more of the two-symbol substrings than it ought to.  In both cases, ÔpumpingÕ has produced words that are not in L.
L is therefore not context-free.
QED
Back to Topic 5
Next Topic

Start of Module

If you have comments or suggestions, email to author at b.cohen@city.ac.uk
or me Vid-Com-Ram / members.tripod.com/bummerang


หมายเหตุ : เอกสารเวปหน้านี้นำมาจากมหาวิทยาลัยแห่งหนึ่งในประเทศอังกฤษ เป็นหลักสูตรคล้ายคลึงกับ CT313 นำมาเพื่อเป็นเอกสารเปรียบเทียบและอ้างอิง มิได้หวังผลประโยชน์ใดๆ และขอบอกว่าเค้ามีลิขสิทธิ์นะ